Shader Learning Notes

Unreal Shader学习

安装及基础概念

知乎《Shader从入门到放弃》在VS中可以安装ShaderToy来观测GLSL
👆这个文字教程也是很不错的

Unreal 5.0 材质中添加自定义 Shader 代码在UE中需要设置Shder文件的位置

<img src=”https://s2.loli.net/2025/09/13/CxzRNf1Witu69IU.png“ alt=”Unreal Sha原本的3D流程应该是：”原画师绘制场景图（将3D场景画下来） -> 建模师根据原画构建场景模型（产出3D模型）-> 程序渲染（将3D模型导入到引擎中，或者其他3D渲染库），然后渲染成画面”。

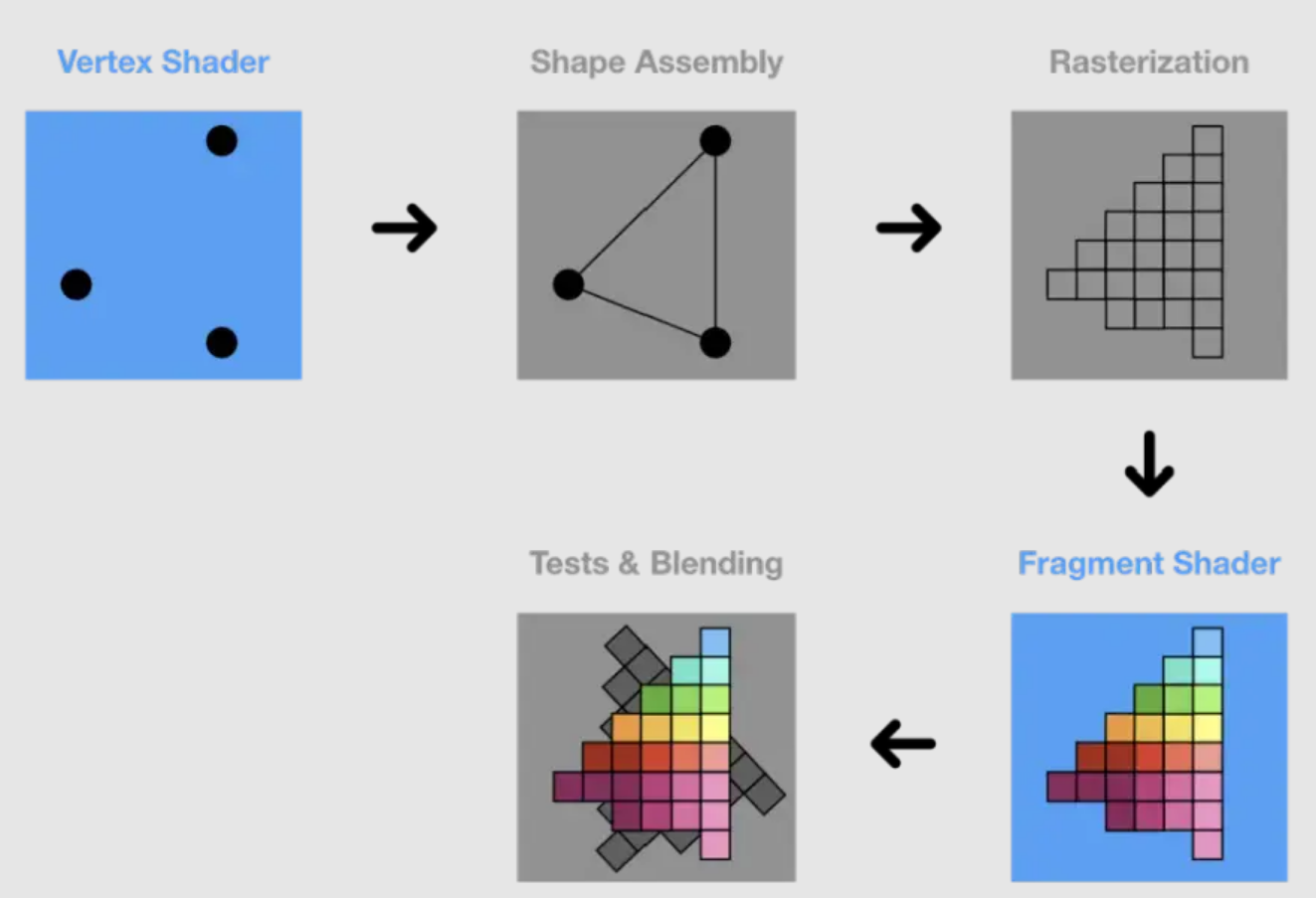
主要是两种着色器：

Fragment Shader（片元shader）：输入插值后的顶点数据，输出最终像素颜色（fragColor）。
Vertex Shader（顶点Shader）：输入单个顶点数据（位置/法线等），输出处理后的顶点位置（gl_Position）和其他插值数据。
compute shader 计算着色器
geometry shader 几何着色器
….

HLSL

基础的语法

min max	最大最小
abs	绝对值
fmod	取余操作
round	四舍五入
pow	指数
sqrt rsqrt	平方根和倒数平方根
degrees（x） redians	弧度转角度角度转弧度
length	向量到原点的距离
frac(sin(dot(uv, float2(12.9898, 78.233))) * 43758.5453);	噪声算法
sin cos tan	三角函数
asin acos atan	他们的反函数
sinh cosh tanh	双曲线函数
ceil	数值范围函数

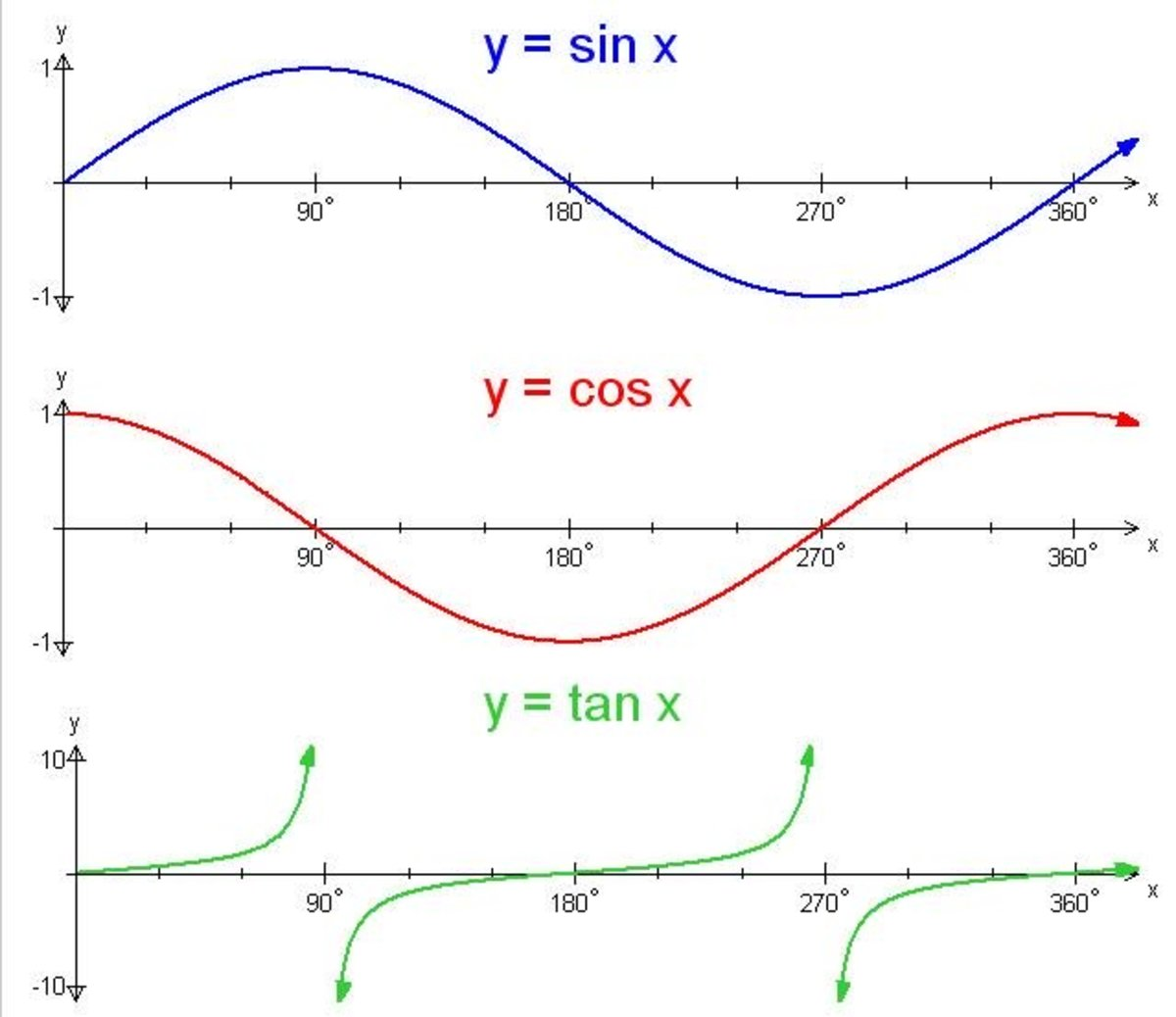
UV坐标系说明:

原点 (0,0) 位于左下角
(0,1) 左上角，(1,1) 右上角，(1,0) 右下角

GLSL

基础语法

step

如果x 小于某个值，则返回 0，如果大于等于这个值，则返回1。

所以上面的代码可以简化成：

// if(abs(uv.x) <= 2. * fwidth(uv.x)) {
//     color = vec3(0.0, 1.0, 0.0);
// }
// ===>

color = step(abs(uv.x), 2.0 * fwidth(uv.x)) * vec3(0.0, 1.0, 0.0);

mix

该函数的实际上执行的就是一个简单的 线性差值。简单的说就是：当a = 1时，返回的值为y, 但a = 0时，返回x的值，如果返回的值为0.5，则返回 0.5x + 0.5y的值，同理，如果a = 0.2, 返回 0.8 * a + 0.2 * y。

我们可以利用这个函数来做颜色叠加，颜色叠加的公式可以写为：
$$
Color=Src.color∗(1−Dst.a)+Dst.color∗Dst.a
$$

smoothstep

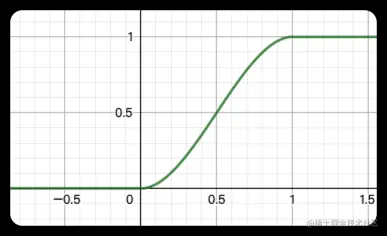
我们可以直观的看出：当x < 0时，返回0，当 x > 1时，返回1，如果 x 处于0~1之间时，则有一个类似于线性插值的过渡，但是请注意，这里并不是线性插值，因为在接近两端的值的时候，该函数有一个平滑的过渡。所以我们可以通过这一点来对 step 函数进行替换以解决锯齿的问题。

floor

作用是向下取整，它会返回不大于输入值的最大整数。例如：对 uv 向量的每个分量（x和y）分别执行向下取整

例如：

1 2	floor(3.7)` → `3.0 floor(-1.2)` → `-2.0

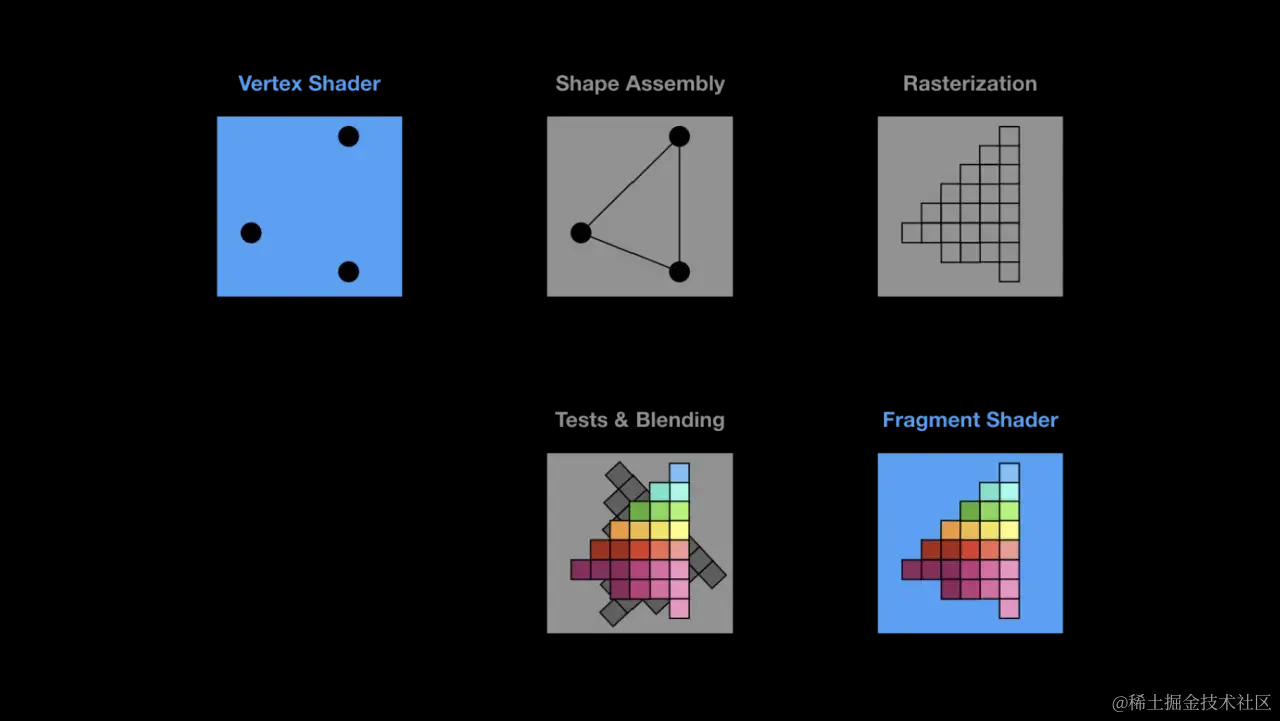
核心步骤（渲染管线）

顶点变换的过程（顶点着色器）
图元装配（按哪种方式装配图元，装配为点，线还是三角形）
光栅化（将上述的图元从矢量图形转换为像素组成的图形）
着色（片段着色器）
测试（Alpha测试，深度测试，模板测试等）& 混合

坐标系

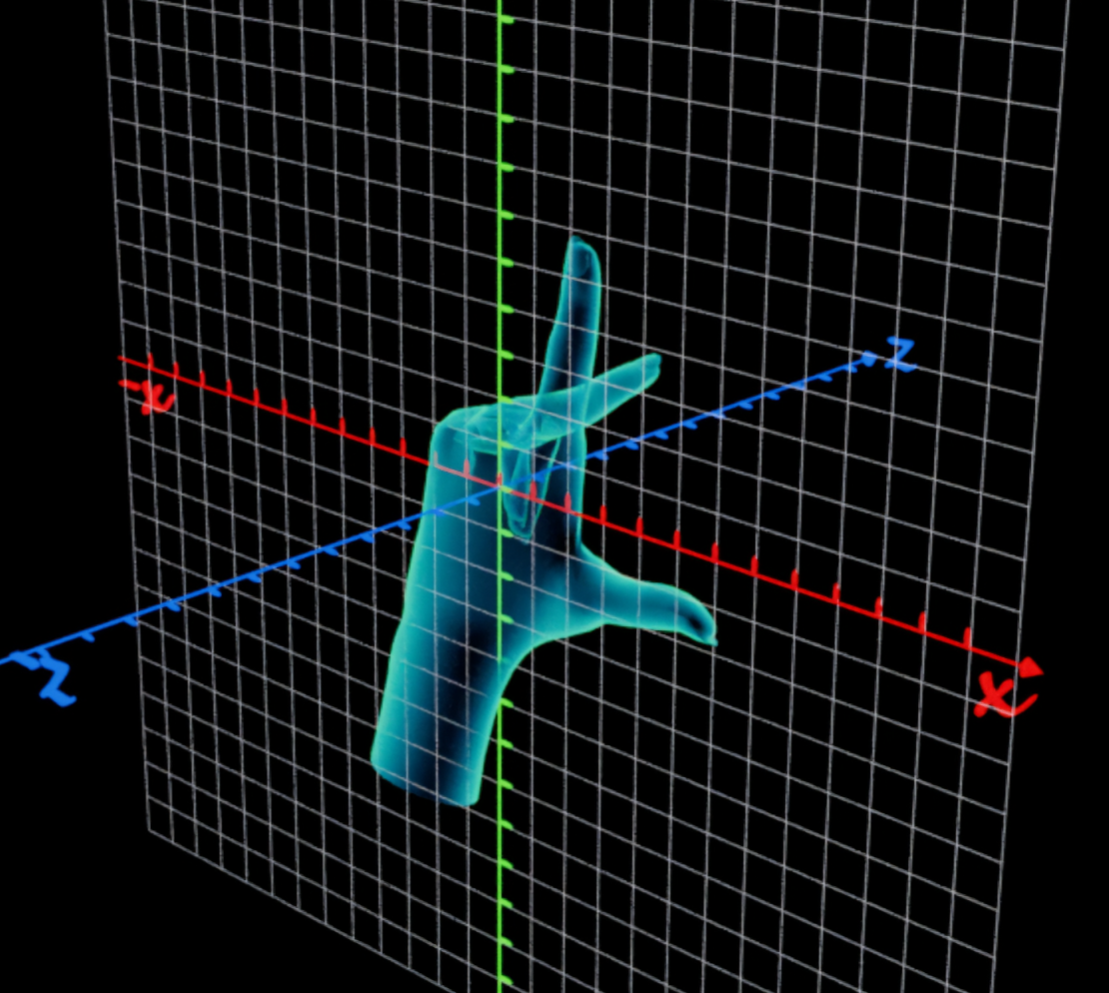
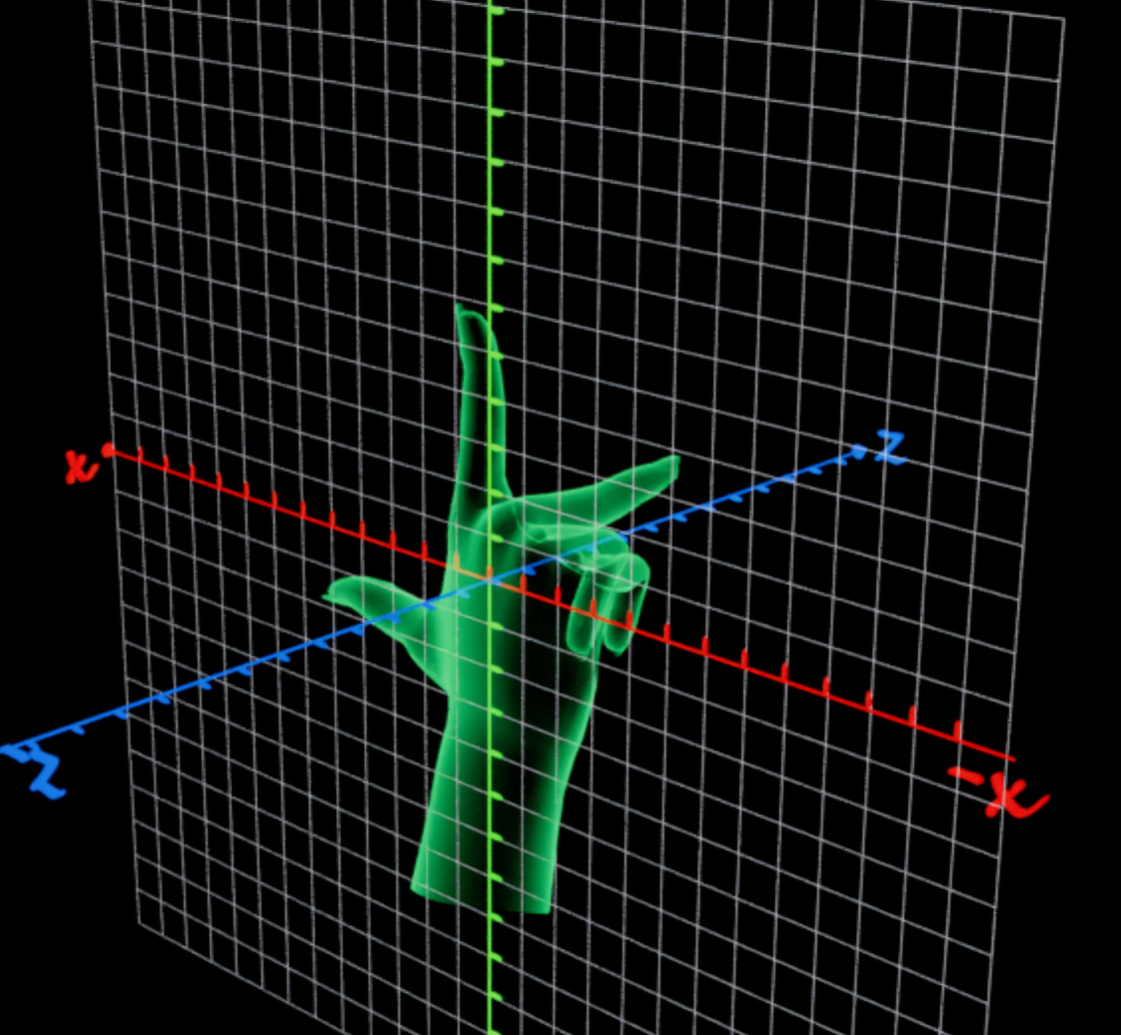
这是左手坐标系反之是右手坐标系

OpenGL是右手坐标系

实现代码

1. 最初始的实例代码（实现一个坐标轴）:

// 归一化uv坐标到[-1,1]范围，保持宽高比
vec2 fixUV(vec2 coord) {
    return 2.0 * (coord - 0.5 * iResolution.xy) / min(iResolution.x, iResolution.y);
}

// 绘制网格线
bool drawGrid(vec2 uv, float scale) {
    // fract(uv * scale)：将坐标按比例缩放后取小数部分，得到每个网格内的相对坐标
    // fwidth(f_uv.x)：计算片段着色器中相邻像素的梯度，即当前像素到下一像素的变化率
    vec2 f_uv = fract(uv * scale);
    // abs(f_uv.x) < fwidth(f_uv.x)：当相对坐标接近 0 时（即网格线位置），返回 true
    return abs(f_uv.x) < fwidth(f_uv.x) || abs(f_uv.y) < fwidth(f_uv.y);
}

// 绘制坐标轴
vec3 drawAxis(vec2 uv) {
    vec3 color = vec3(0.0);
    
    if(abs(uv.x) < fwidth(uv.x)) {
        color = vec3(0.0, 1.0, 0.0); // x轴为绿色
    }
    
    if(abs(uv.y) < fwidth(uv.y)) {
        color = vec3(1.0, 0.0, 0.0); // y轴为红色
    }
    
    return color;
}

// 主函数
void mainImage(out vec4 fragColor, in vec2 fragCoord) {
    // 归一化坐标
    vec2 uv = fixUV(fragCoord);
    
    // 基础背景色
    vec3 color = vec3(0.0);
    
    // 绘制网格
    if(drawGrid(uv, 3.0)) {
        color = vec3(1.0);
    }
    
    // 绘制坐标轴（会覆盖网格线）
    vec3 axisColor = drawAxis(uv);
    if(axisColor != vec3(0.0)) {
        color = axisColor;
    }
    
    fragColor = vec4(color, 1.0);
}

https://www.shadertoy.com/view/Wf2fRw
这个shader创建了一个坐标系统，包含网格线和彩色坐标轴。

2. 实现函数的y=kx的绘制

// 归一化uv坐标到[-1,1]范围，保持宽高比
vec2 fixUV(vec2 coord) {
    return 2.0 * (coord - 0.5 * iResolution.xy) / min(iResolution.x, iResolution.y);
}

// 绘制网格线
bool drawGrid(vec2 uv, float scale) {
    vec2 f_uv = fract(uv * scale);
    return abs(f_uv.x) < fwidth(f_uv.x) || abs(f_uv.y) < fwidth(f_uv.y);
}

// 绘制坐标轴
vec3 drawAxis(vec2 uv) {
    vec3 color = vec3(0.0);
    
    if(abs(uv.x) < fwidth(uv.x)) {
        color = vec3(0.0, 1.0, 0.0); // x轴为绿色
    }
    
    if(abs(uv.y) < fwidth(uv.y)) {
        color = vec3(1.0, 0.0, 0.0); // y轴为红色
    }
    
    return color;
}

// 计算点到直线距离的向量实现
// 这个函数计算点p到线段ab的最短距离
// a、b是线段的两个端点
float distLine(vec2 p, vec2 a, vec2 b) {
    vec2 ab = b - a;
    vec2 ap = p - a;
    vec2 ad = dot(ab, ap) / dot(ab, ab) * ab;
    return length(ap - ad);
}

// 主函数
void mainImage(out vec4 fragColor, in vec2 fragCoord) {
    // 旧的部分
    vec2 uv = fixUV(fragCoord);
    vec3 color = vec3(0.0);
    if(drawGrid(uv, 10.0)) {
        color = vec3(1.0);
    }
    vec3 axisColor = drawAxis(uv);
    if(axisColor != vec3(0.0)) {
        color = axisColor;
    }
    
    float d = distLine(uv, vec2(0.0), vec2(1.0));
    color = mix(color, vec3(0.0,0.0,1.0), smoothstep(0.002, 0.001, d));
    fragColor = vec4(color, 1.0);
}

https://www.shadertoy.com/view/3c2fzw

3. 实现一段复杂函数的绘制（分段绘制）

#define PI 3.1415926
#define STEP 1.0

vec2 fixUV(vec2 coord) {
    return 3.0 * (2. * (coord.xy - 0.5 * iResolution.xy) / min(iResolution.x, iResolution.y));
}

vec3 grid(vec2 uv) {
    vec3 color = vec3(0.95);

    vec2 cell = 1.0 - 2.0 * abs(fract(uv) - 0.5);
    color = mix(color, vec3(0.7), step(cell.x, 4.0 * fwidth(uv.x)));
    color = mix(color, vec3(0.7), smoothstep(4.0 * fwidth(uv.y), 3.9 * fwidth(uv.y), cell.y));
    color = mix(color, vec3(0.3, 0.7, 0.8), smoothstep(2.0 * fwidth(uv.x), 1.9 * fwidth(uv.x), abs(uv.x)));
    color = mix(color, vec3(1.0, 0.5, 0.0), smoothstep(2.0 * fwidth(uv.x), 1.9 * fwidth(uv.y), abs(uv.y)));

    return color;
}

float func(in float x) {
    return sin(x + sin(x + sin(x) * 0.8));
}

float distLine(vec2 p, vec2 a, vec2 b) {
    vec2 ab = b - a;
    vec2 ap = p - a;
    vec2 ad = clamp(dot(ab, ap) / dot(ab, ab), 0.0, 1.0) * ab;
    return length(ap - ad);
}

// 它是一个数学计算函数，返回的是一个表示"线段影响值"的浮点数。
// 返回的 float 值表示当前像素(uv)与线段的接近程度
// 值范围在 0.0 到 1.0 之间：
// 0.0 表示像素完全在线段之外
// 1.0 表示像素正好在线段上
// 中间值表示像素在线段附近(有抗锯齿效果)
float segment(vec2 p, vec2 a, vec2 b, float w) {
    float f = 0.0;
    vec2 ab = b - a;
    vec2 ap = p - a;
    float proj = clamp(dot(ab, ap) / dot(ab, ab), 0.0, 1.0);
    float d = length(ap - proj * ab);
    f = smoothstep(w, w * 0.2, d);
    return f;
}

float plotFunc(in vec2 uv) {
    float f = 0.0;
    // 这是一个从 0 到屏幕宽度(iResolution.x)的循环
    // STEP 是步长(已定义为 1.0)，控制采样点的密度
    for(float x = 0.0; x <= iResolution.x; x += STEP) {
        // 上一个点的坐标
        float fx = fixUV(vec2(x, 0.0)).x;
        // 下一个点的坐标
        float nfx = fixUV(vec2(x + STEP, 0.0)).x;
        f += segment(uv, vec2(fx, func(fx)), vec2(nfx, func(nfx)), 0.006);
    }
    return f;
}

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
    // old
    vec2 uv = fixUV(fragCoord.xy);
    vec3 color = grid(uv);

    float f = plotFunc(uv);
    color = mix(color, vec3(0.0, 0.0, 0.0), f);
    fragColor = vec4(color, 1.0);
}

https://www.shadertoy.com/view/Wc2fzw

4. 实现一个（静态）星芒效果

#define PI 3.1415926
#define STEP 1.0

vec2 fixUV(vec2 coord) {
    return 4.0 * (2. * (coord.xy - 0.5 * iResolution.xy) / min(iResolution.x, iResolution.y));
}

vec3 grid(vec2 uv) {
    // 坐标外其他颜色绘制改变
    vec3 color = vec3(0.0);
    color.rg = fract(uv);

    vec2 cell = 1.0 - 2.0 * abs(fract(uv) - 0.5);
    // 网格纵向
    color = mix(color, vec3(0.7), step(cell.x, 4.0 * fwidth(uv.x)));
    // 网格横向
    color = mix(color, vec3(0.7), smoothstep(4.0 * fwidth(uv.y), 3.9 * fwidth(uv.y), cell.y));
    // 纵向坐标轴
    color = mix(color, vec3(0.3, 0.7, 0.8), smoothstep(2.0 * fwidth(uv.x), 1.9 * fwidth(uv.x), abs(uv.x)));
    // 横向坐标轴
    color = mix(color, vec3(1.0, 0.5, 0.0), smoothstep(2.0 * fwidth(uv.x), 1.9 * fwidth(uv.y), abs(uv.y)));

    return color;
}

float func(in float x) {
    return sin(x + sin(x + sin(x) * 0.8));
}

float distLine(vec2 p, vec2 a, vec2 b) {
    vec2 ab = b - a;
    vec2 ap = p - a;
    vec2 ad = clamp(dot(ab, ap) / dot(ab, ab), 0.0, 1.0) * ab;
    return length(ap - ad);
}

float Line(vec2 p, vec2 a, vec2 b) {
    float d = distLine(p, a, b);
    float m = smoothstep(0.02, 0.01, d);
    return m;
}

float segment(vec2 p, vec2 a, vec2 b, float w) {
    float f = 0.0;
    vec2 ab = b - a;
    vec2 ap = p - a;
    float proj = clamp(dot(ab, ap) / dot(ab, ab), 0.0, 1.0);
    float d = length(ap - proj * ab);
    f = smoothstep(w, w * 0.2, d);
    return f;
}

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
    vec2 uv = fixUV(fragCoord.xy);

    // 修改了绘制坐标的函数
    vec3 Basecolor = grid(uv);

    // 小坐标位置中心点弄到方块的中心
    vec2 st = fract(uv) - 0.5;
    

    // 创建3x3点阵
    int i = 0;
    vec2 p[9];
    for(float y = -1.0; y <= 1.0; y++) {
        for(float x = -1.0; x <= 1.0; x++) {
            vec2 offs = vec2(x, y);
            p[i++] = offs;
        }
    }

    // 连线绘制 (使用蓝色)
    float m2 = 0.0;
    for(i = 0; i < 9; i++) {
        m2 += Line(st, p[i], p[4]);
    }
    Basecolor = mix(Basecolor, vec3(0.0, 0.0, 1.0), m2); // 绘制连线
    
    // 绘制每个区域中间的点 (使用红色)
    float d = length(st);
    float m1 = smoothstep(0.1, 0.09, d);
    Basecolor = mix(Basecolor, vec3(1.0), m1); // 绘制点


    fragColor = vec4(Basecolor, 1.0);
    return;
}

5. 随机数生成办法

vec2 N22(vec2 p) {

    // 任意的大数字 但还是有一些要求：
    // 你可以替换为其他大数（如 vec2(123.45, 678.90)）
    // 但需要避免：
    // 过于简单的数字（如 100.0, 200.0）
    // 互为倍数的数字（如 50.0, 100.0）
    // 与后续魔法数字（123.34等）有简单数学关系的数字
    p += vec2(434.67, 534.23);  

    // 将2D坐标扩展为3D向量 p.xyx（如输入(x,y)变为(x,y,x)）
    // 乘以精心选择的"魔法数字"向量（这些质数增加混乱度）
    // fract() 取小数部分，确保数值在[0,1)范围内
    vec3 a = fract(p.xyx * vec3(123.34, 234.34, 345.65));

    // 计算向量点积并叠加到自身（dot(a,a)计算自相关）
    // 添加34.45偏移避免对称性
    // 这步大幅增加输出的随机性
    a += dot(a, a + 34.45);

    return fract(vec2(a.x * a.y, a.y * a.z));
}

vec2 fixUV(vec2 coord) {
    return 3.0 * (2. * (coord.xy - 0.5 * iResolution.xy) / min(iResolution.x, iResolution.y));
}

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
    vec2 uv = fixUV(fragCoord.xy);

    vec2 n = N22(uv);
    fragColor = vec4(n, 0.0, 1.0);
}

6. 星星连线效果

#define PI 3.1415926
#define STEP 1.0

vec2 fixUV(vec2 coord) {
    return 5.0 * (2. * (coord.xy - 0.5 * iResolution.xy) / min(iResolution.x, iResolution.y));
}

float distLine(vec2 p, vec2 a, vec2 b) {
    vec2 ab = b - a;
    vec2 ap = p - a;
    vec2 ad = clamp(dot(ab, ap) / dot(ab, ab), 0.0, 1.0) * ab;
    return length(ap - ad);
}

float Line(vec2 p, vec2 a, vec2 b) {
    float d = distLine(p, a, b);  // 计算点p到线段ab的距离
    float m = smoothstep(0.02, 0.01, d); // 第一次渐变：生成线宽
    float d2 = length(a - b);     // 计算线段ab的长度
    m *= smoothstep(1.2, 1.1, d2);// 第二次渐变：控制线段显隐
    return m;
}

vec2 N22(vec2 p) {
    p += vec2(434.67, 534.23);
    vec3 a = fract(p.xyx * vec3(123.34, 234.34, 345.65));
    a += dot(a, a + 34.45);
    return fract(vec2(a.x * a.y, a.y * a.z));
}

vec3 N23_to_3(vec2 p) {
    // First layer hash
    vec3 a = fract(p.xyx * vec3(123.34, 234.34, 345.65));
    a += dot(a, a.yxz + 34.45);
    
    // Second layer hash (using rotated coordinates)
    vec3 b = fract(p.yxy * vec3(456.78, 567.89, 678.91)); 
    b += dot(b, b.zxy + 45.67);
    
    // Combine layers
    vec3 r = fract(vec3(
        a.x * b.y,
        a.y * b.z,
        a.z * b.x
    ));
    
    // Final mixing
    return fract(r * 0.5 + 0.5);
}

vec2 GetPos(vec2 id, vec2 offs) {
    // 根据格子的 id和offs 产生一个随机数，
    // 乘上iTime使其根据时间发生变化
    vec2 n = N22(id + offs) * iTime * 6.11; // 6.11是一个调节速度的数值
    return sin(n) * 0.4 + offs;
}

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
    
    vec2 uv = fixUV(fragCoord.xy);
    // 修改了绘制坐标的函数
    vec3 Basecolor = vec3(0.0);
    // 小坐标位置中心点弄到方块的中心
    vec2 st = fract(uv) - 0.5;
    
    // 获取到格子的中心轴点
    vec2 id = floor(uv);
    vec3 idcolor = N23_to_3(id);

    // 创建3x3点阵
    int i = 0;
    vec2 p[9];
    for(float y = -1.0; y <= 1.0; y++) {
        for(float x = -1.0; x <= 1.0; x++) {
            vec2 offs = vec2(x, y);
            p[i++] = GetPos(id, offs);
        }
    }

    // 连线绘制 (使用蓝色)
    float m2 = 0.0;
    for(i = 0; i < 9; i++) {
        m2 += Line(st, p[i], p[4]);

     
        // 画星星 中间闪烁部分
        float d = length(st - p[i]);
        float spark = 1.0 / (d * d * 200.0) * (sin(iTime * 13.0 + p[i].x * 17.0) * 0.4 + 0.6);
        m2 += spark;

        // 这一部分会断开 重新连接
        m2 += Line(st, p[1], p[3]);
        m2 += Line(st, p[1], p[5]);
        m2 += Line(st, p[7], p[3]);
        m2 += Line(st, p[7], p[5]);
    }

    Basecolor = mix(Basecolor, idcolor, m2); // 绘制连线
    
    fragColor = vec4(Basecolor, 1.0);
    return;
}

7. 星星推进（博主的版本）

vec2 N22(vec2 p) {
    p += vec2(434.67, 534.23);
    vec3 a = fract(p.xyx * vec3(123.34, 234.34, 345.65));
    a += dot(a, a + 34.45);
    return fract(vec2(a.x * a.y, a.y * a.z));
}

float DistLine(vec2 p, vec2 a, vec2 b) {
    vec2 pa = p - a;
    vec2 ba = b - a;
    float t = clamp(dot(pa, ba) / dot(ba, ba), 0.0, 1.0);
    return length(pa - ba * t);
}

vec2 GetPos(vec2 id, vec2 offs) {
    vec2 n = N22(id + offs) * iTime;
    return sin(n) * 0.4 + offs;
}

float Line(vec2 p, vec2 a, vec2 b) {
    float d = DistLine(p, a, b);
    float m = smoothstep(0.02, 0.01, d);
    float d2 = length(a - b);
    m *= smoothstep(1.2, 0.8, d2) + smoothstep(0.05, 0.03, abs(d2 - 0.75));
    return m;
}

float Layer(vec2 uv) {
    vec2 st = fract(uv) - 0.5;
    vec2 id = floor(uv);
    float m = 0.0;

    int i = 0;
    vec2 p[9];
    for(float y = -1.0; y <= 1.0; y++) {
        for(float x = -1.0; x <= 1.0; x++) {
            vec2 offs = vec2(x, y);
            p[i++] = GetPos(id, offs);
        }
    }
    float t = iTime;
    for(i = 0; i < 9; i++) {
        m += Line(st, p[i], p[4]);
        // vec2 j = (st - p[i]) * 20.0;
        float d = length(st - p[i]);
        float spark = 1.0 / (d * d * 200.0) * (sin(t * 13.0 + p[i].x * 17.0) * 0.4 + 0.6);
        m += spark;
    }

    m += Line(st, p[1], p[3]);
    m += Line(st, p[1], p[5]);
    m += Line(st, p[7], p[3]);
    m += Line(st, p[7], p[5]);
    return m;
}

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
    vec2 uv = (fragCoord.xy - .5 * iResolution.xy) / iResolution.y;
    vec3 col = vec3(0);
    float m = 0.0;
    float t = iTime * 0.1;
    for(float i = 0.0; i <= 1.0; i += 1. / 4.) {
        float depth = fract(i + t);
        float size = mix(15.0, 0.5, depth);
        float fade = smoothstep(0.0, 0.2, depth) * smoothstep(0.9, 0.8, depth);
        m += Layer(uv * size + i * 20.0) * fade;
    }

    t *= 5.0;
    float gradinet = uv.y;
    vec3 baseCol = vec3(0.323, 0.456, 0.567);
    col = m * baseCol * (sin(t) * 0.4 + 0.8);
    col -= baseCol * gradinet;
    fragColor = vec4(col, 1.0);
}

8.一个最简单的3D点

原本的3D流程应该是：“原画师绘制场景图（将3D场景画下来） -> 建模师根据原画构建场景模型（产出3D模型）-> 程序渲染（将3D模型导入到引擎中，或者其他3D渲染库），然后渲染成画面”。

我们简要回顾一下：

顶点变换的过程（顶点着色器）
图元装配（按哪种方式装配图元，装配为点，线还是三角形）
光栅化（将上述的图元从矢量图形转换为像素组成的图形）
着色（片段着色器）
测试（Alpha测试，深度测试，模板测试等）& 混合

通过上述方式渲染的3D模型的方式我们通常称为光栅化的方法

而在我们的shadertoy中，我们是直接在片段着色器中进行编程，我们只有上述的第四与第五步的过程。其实相当于我们现在变成了原画师，我们需要在一张纸上做画，而且画的是3D场景。好在我们还有另一种构建3D场景的方式，就是光线追踪或光线步进。

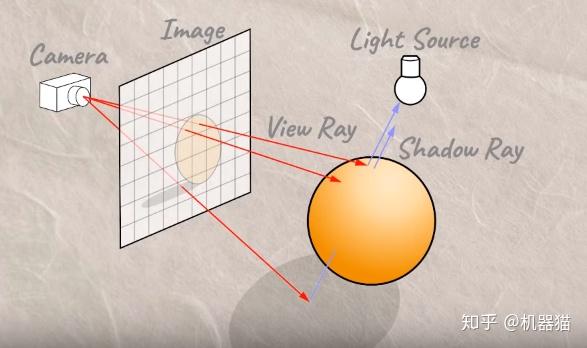
https://juejin.cn/post/7362059823662432306

// 点p到直线ro到rd的距离
float DistLine(vec3 ro, vec3 rd, vec3 p) {
    return length(cross(p - ro, rd) / length(rd));      // 使用向量叉积公式计算点到直线的距离：(p-ro)与rd的叉积长度除以rd的长度
}
 
void mainImage(out vec4 fragColor, in vec2 fragCoord) {
    vec2 uv = fragCoord.xy / iResolution.xy;// 将像素坐标归一化到[0,1]范围
    uv -= 0.5;// 将坐标原点移到屏幕中心(范围变为[-0.5,0.5])
    uv.x *= iResolution.x / iResolution.y;// 修正宽高比，防止图像变形

    vec3 ro = vec3(0., 0., -1.);// 定义摄像机（观察点）位置(ray origin)在z=-1处
    vec3 rd = vec3(uv.x, uv.y, 0.0) - ro;// 计算从摄像机到当前像素的射线方向(ray direction)

    float t = iGlobalTime; //定义一个变量，方便让球动起来
    vec3 p = vec3(sin(t), 0., 3.0); // 定义球的位置
    float r = 0.01; // 定义球的半径

    float d = DistLine(ro, rd, p); // 计算球心与观察射线之间的距离
    d = smoothstep(r + 0.01, r, d); // 若距离小于半径，d 则等于1。
    fragColor = vec4(d, d, d, 1.0); // 将球着色为白色
}

100.一个海Shader（优化版本）

/*
 * "Seascape" by Alexander Alekseev aka TDM - 2014
 * License Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
 * Contact: tdmaav@gmail.com
 */

const int NUM_STEPS = 32;
const float PI	 	= 3.141592;
const float EPSILON	= 1e-3;
#define EPSILON_NRM (0.1 / iResolution.x)
//#define AA

// sea
const int ITER_GEOMETRY = 3;
const int ITER_FRAGMENT = 5;
const float SEA_HEIGHT = 0.6;
const float SEA_CHOPPY = 4.0;
const float SEA_SPEED = 0.8;
const float SEA_FREQ = 0.16;
const vec3 SEA_BASE = vec3(0.0,0.09,0.18);
const vec3 SEA_WATER_COLOR = vec3(0.8,0.9,0.6)*0.6;
#define SEA_TIME (1.0 + iTime * SEA_SPEED)
const mat2 octave_m = mat2(1.6,1.2,-1.2,1.6);

// math
mat3 fromEuler(vec3 ang) {
	vec2 a1 = vec2(sin(ang.x),cos(ang.x));
    vec2 a2 = vec2(sin(ang.y),cos(ang.y));
    vec2 a3 = vec2(sin(ang.z),cos(ang.z));
    mat3 m;
    m[0] = vec3(a1.y*a3.y+a1.x*a2.x*a3.x,a1.y*a2.x*a3.x+a3.y*a1.x,-a2.y*a3.x);
	m[1] = vec3(-a2.y*a1.x,a1.y*a2.y,a2.x);
	m[2] = vec3(a3.y*a1.x*a2.x+a1.y*a3.x,a1.x*a3.x-a1.y*a3.y*a2.x,a2.y*a3.y);
	return m;
}
float hash( vec2 p ) {
	float h = dot(p,vec2(127.1,311.7));	
    return fract(sin(h)*43758.5453123);
}
float noise( in vec2 p ) {
    vec2 i = floor( p );
    vec2 f = fract( p );
    // Add distance-based smoothing
    float dist = length(p);
    float smoothFactor = smoothstep(0.0, 5.0, dist);
    vec2 u = mix(f, f*f*(3.0-2.0*f), smoothFactor);
    return -1.0+2.0*mix( mix( hash( i + vec2(0.0,0.0) ), 
                     hash( i + vec2(1.0,0.0) ), u.x),
                mix( hash( i + vec2(0.0,1.0) ), 
                     hash( i + vec2(1.0,1.0) ), u.x), u.y);
}

// lighting
float diffuse(vec3 n,vec3 l,float p) {
    return pow(dot(n,l) * 0.4 + 0.6,p);
}
float specular(vec3 n,vec3 l,vec3 e,float s) {    
    float nrm = (s + 8.0) / (PI * 8.0);
    return pow(max(dot(reflect(e,n),l),0.0),s) * nrm;
}

// sky
vec3 getSkyColor(vec3 e) {
    e.y = (max(e.y,0.0)*0.8+0.2)*0.8;
    return vec3(pow(1.0-e.y,2.0), 1.0-e.y, 0.6+(1.0-e.y)*0.4) * 1.1;
}

// sea
float sea_octave(vec2 uv, float choppy) {
    uv += noise(uv);        
    vec2 wv = 1.0-abs(sin(uv));
    vec2 swv = abs(cos(uv));    
    wv = mix(wv,swv,wv);
    return pow(1.0-pow(wv.x * wv.y,0.65),choppy);
}

float map(vec3 p) {
    float freq = SEA_FREQ;
    float amp = SEA_HEIGHT;
    float choppy = SEA_CHOPPY;
    vec2 uv = p.xz; uv.x *= 0.75;
    
    float d, h = 0.0;    
    for(int i = 0; i < ITER_GEOMETRY; i++) {        
    	d = sea_octave((uv+SEA_TIME)*freq,choppy);
    	d += sea_octave((uv-SEA_TIME)*freq,choppy);
        h += d * amp;        
    	uv *= octave_m; freq *= 1.9; amp *= 0.22;
        choppy = mix(choppy,1.0,0.2);
    }
    return p.y - h;
}

float map_detailed(vec3 p) {
    float freq = SEA_FREQ;
    float amp = SEA_HEIGHT;
    float choppy = SEA_CHOPPY;
    vec2 uv = p.xz; uv.x *= 0.75;
    
    float d, h = 0.0;    
    for(int i = 0; i < ITER_FRAGMENT; i++) {        
    	d = sea_octave((uv+SEA_TIME)*freq,choppy);
    	d += sea_octave((uv-SEA_TIME)*freq,choppy);
        h += d * amp;        
    	uv *= octave_m; freq *= 1.9; amp *= 0.22;
        choppy = mix(choppy,1.0,0.2);
    }
    return p.y - h;
}

vec3 getSeaColor(vec3 p, vec3 n, vec3 l, vec3 eye, vec3 dist) {  
    float fresnel = clamp(1.0 - dot(n, -eye), 0.0, 1.0);
    fresnel = min(fresnel * fresnel * fresnel, 0.5);
    
    vec3 reflected = getSkyColor(reflect(eye, n));    
    vec3 refracted = SEA_BASE + diffuse(n, l, 80.0) * SEA_WATER_COLOR * 0.12; 
    
    vec3 color = mix(refracted, reflected, fresnel);
    
    float atten = max(1.0 - dot(dist, dist) * 0.001, 0.0);
    color += SEA_WATER_COLOR * (p.y - SEA_HEIGHT) * 0.18 * atten;
    
    color += specular(n, l, eye, 60.0);
    
    return color;
}

// tracing
vec3 getNormal(vec3 p, float eps) {
        // Distance-based eps adjustment
    float dist = length(p);
    eps = mix(eps*0.5, eps*2.0, smoothstep(0.0, 10.0, dist));
    
    vec3 n;
    n.y = map_detailed(p);    
    n.x = map_detailed(vec3(p.x+eps,p.y,p.z)) - n.y;
    n.z = map_detailed(vec3(p.x,p.y,p.z+eps)) - n.y;
    n.y = eps;
    
    // Smooth normal
    return normalize(mix(n, vec3(0,1,0), 0.1 * smoothstep(0.0, 5.0, dist)));
}

float heightMapTracing(vec3 ori, vec3 dir, out vec3 p) {  
    float tm = 0.0;
    float tx = 1000.0;    
    float hx = map(ori + dir * tx);
    if(hx > 0.0) {
        p = ori + dir * tx;
        return tx;   
    }
    float hm = map(ori);    
    for(int i = 0; i < NUM_STEPS; i++) {
        float tmid = mix(tm, tx, hm / (hm - hx));
        p = ori + dir * tmid;
        float hmid = map(p);        
        if(hmid < 0.0) {
            tx = tmid;
            hx = hmid;
        } else {
            tm = tmid;
            hm = hmid;
        }        
        if(abs(hmid) < EPSILON) break;
    }
    return mix(tm, tx, hm / (hm - hx));
}

vec3 getPixel(in vec2 coord, float time) {    
    vec2 uv = coord / iResolution.xy;
    uv = uv * 2.0 - 1.0;
    uv.x *= iResolution.x / iResolution.y;    
        
    // ray
    vec3 ang = vec3(sin(time*3.0)*0.1,sin(time)*0.2+0.3,time);    
    vec3 ori = vec3(0.0,3.5,time*5.0);
    vec3 dir = normalize(vec3(uv.xy,-2.0)); dir.z += length(uv) * 0.14;
    dir = normalize(dir) * fromEuler(ang);
    
    // tracing
    vec3 p;
    heightMapTracing(ori,dir,p);
    vec3 dist = p - ori;
    vec3 n = getNormal(p, dot(dist,dist) * EPSILON_NRM);
    vec3 light = normalize(vec3(0.0,1.0,0.8)); 
             
    // color
    return mix(
        getSkyColor(dir),
        getSeaColor(p,n,light,dir,dist),
    	pow(smoothstep(0.0,-0.02,dir.y),0.2));
}

// main
void mainImage( out vec4 fragColor, in vec2 fragCoord ) {
    float time = iTime * 0.3 + iMouse.x*0.01;
	
#ifdef AA
    vec3 color = vec3(0.0);
    for(int i = -1; i <= 1; i++) {
        for(int j = -1; j <= 1; j++) {
        	vec2 uv = fragCoord+vec2(i,j)/3.0;
    		color += getPixel(uv, time);
        }
    }
    color /= 9.0;
#else
    vec3 color = getPixel(fragCoord, time);
#endif
    
    // post
	fragColor = vec4(pow(color,vec3(0.65)), 1.0);
}

ShaderToy

常用的全局变量

* ⚠️警告

尽可能不要在Shader中写 If 逻辑代码，因为不能充分发挥SIMD的性能

* 其他专有名词解释

齐次坐标：用 n + 1 维向量来表示 n 维向量。比如在 2D 中，点 (x, y) 用 (x, y, w) 表示，w 通常为 1，若 w = 0 则表示无穷远点；在 3D 里，点 (x, y, z) 表示为 (x, y, z, w) 。它能简化图形学计算，还可表示无穷远点。